DeepStochLog is a neural-symbolic framework for neural stochastic logic programming. This framework allows users to express background knowledge using logic and probabilities to train neural networks more effectively. It achieved state-of-the-art results on a wide variety of tasks while scaling much better than alternative neural-symbolic frameworks.

For more in-depth, see the DeepStochLog Github repository and the DeepStochLog paper.

Capabilities

Sum of handwritten numbers

For example, consider having to calculate the sum of two handwritten numbers, but never having seen handwritten numbers with their numeric label, but only having seen combinations of handwritten numbers together with their numerical sum.

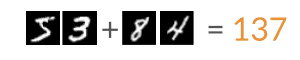
DeepStochLog encodes this information as follows:

digit_dom(Y) :- member(Y,[0,1,2,3,4,5,6,7,8,9]).

nn(number, [X], Y, digit_dom) :: digit(Y) --> [X].
1 :: addition(N) --> digit(N1),
                     digit(N2),
                     {N is N1 + N2}.

General tasks

More generally, DeepStochLog can easily parse and classify sequences of subsymbolic information like images that follow a known grammar structure. It can even encode general problems like word algebra problems, labeling papers in a citation graph, or any other task that could be expressed using neural stochastic logic.

In our experiments in the paper, we found that DeepStochLog achieved state-of-the-art accuracy for all tasks but scaled better than similar neural-symbolic frameworks.

Defining Neural Definite Clause Grammars

Rules in DeepStochLog are modeled as grammar rules that are allowed to contain arguments, logic, and (neural) probabilities.

nn(m,[I1,…,Im],[O1,…,OL],[D1,…,DL]) :: nt --> g1, …, gn.

Where:

• nt is an atom
• g1,…,gn are goals (goal = atom or list of terminals & variables)
• I1,…,Im and O1,…,OL are variables occurring in g1,…,gn and are the inputs and outputs of m
• D1,…,DL are the predicates specifying the domains of O1,…,OL
• m is a neural network mapping I1,…,Im to probability distribution over O1,…,OL (= over cross product of D1,…,DL)

Understanding Neural Definite Clause Grammars

DeepStochLog extends definite clause grammars with neural probabilities to create "Neural Definite Clause Grammars". To understand this, let's look at the basic building blocks, namely context-free grammars and probabilistic context-free grammars, as well as its logic-based extensions, definite clause grammars, and stochastic definite clause grammars.

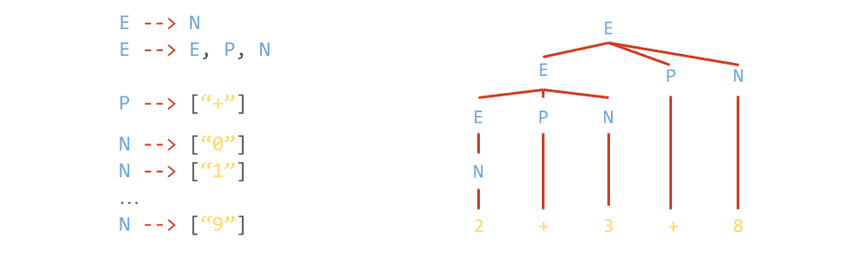
Context-free grammars

Context-free grammars model rules as just mappings from non-terminals to sequences of other non-terminals and terminals. It is helpful for a wide variety of language tasks, such as:

• Finding out if a sequence is an element of the specified language
• Labeling the "part of speech"-tag of a terminal
• Generating all elements of language

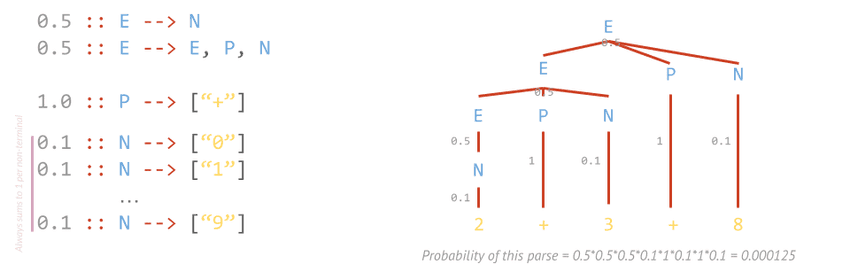
Probabilistic context-free grammars

Probabilistic context-free grammars extend context-free grammars by adding probabilities to every rule. The probabilities of all used rules in the expansion are then used to calculate the probability of a particular parse. This framework helps find answers to the following questions:

• What is the most likely parse for this sequence of terminals? (useful for ambiguous grammars)
• What is the probability of generating this string?

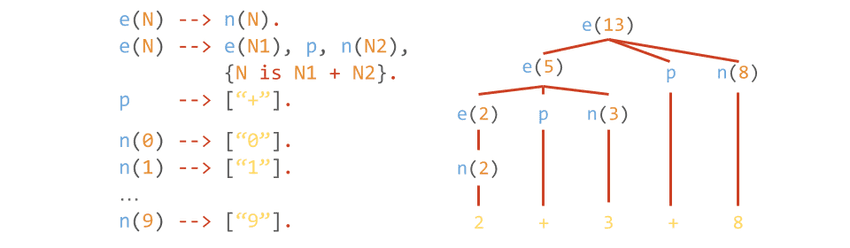
Definite clause grammars

Definite clause grammars extend context-free grammars with logic programming concepts. It allows for adding arguments to the non-terminals and extra logic calculations between the curly brackets {}. The addition of logic programming makes this type of grammar Turing-complete.

Definite clause grammars are helpful for:

• Modelling more complex languages (e.g. context-sensitive)
• Adding constraints between non-terminals thanks to Prolog power (e.g., through unification)
• Extra inputs & outputs aside from terminal sequence (through unification of input variables)

Stochastic definite clause grammars

Stochastic definite clause grammars add the same benefit to definite clause grammars as probabilistic context-free grammars add to context-free grammars, namely adding probabilities to rules. These grammars thus give rise to the same benefits, like finding the most likely parse. However, since expansions can fail in a definite clause grammar, probability mass can get lost in such a failing derivation, meaning that the sum of the probabilities of all possible elements is not necessarily 1.

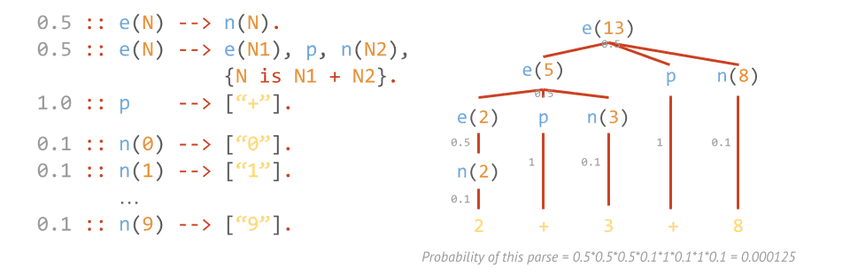
Neural definite clause grammars

Neural definite clause grammars add neural probabilities to stochastic definite clause grammars, which swap rule probabilities with neural networks that output a probability. This is the same trick as DeepProbLog does to probabilistic logic programming, but then to stochastic definite clause grammars.

This framework is helpful for:

• Subsymbolic processing: e.g. tensors as terminals
• Learning rule probabilities using neural networks

Paper

If you would like to refer to this work, or if you use this work in an academic context, please consider citing the following paper:

@article{winters2021deepstochlog,
  title={Deepstochlog: Neural stochastic logic programming},
  author={Winters, Thomas and Marra, Giuseppe and Manhaeve, Robin and De Raedt, Luc},
  journal={arXiv preprint arXiv:2106.12574},
  year={2021}
}

Or APA style:

Winters, T., Marra, G., Manhaeve, R., & De Raedt, L. (2021). Deepstochlog: Neural stochastic logic programming. arXiv Preprint arXiv:2106.12574.